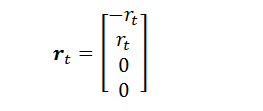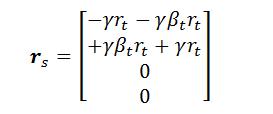Lienard-Wiechert Potentials

Lienard-Wiechert Potentials

We have been assuming the electrostatic potential:

but if the source and test charges are moving with respect to each other, in which frame is r calculated?  In particular, do we use the r value in the test charge frame or the source charge frame?  If the charges are moving these are two different values. 

Consider two particles, a stationary test charge, q_t, and a moving source charge, q_s at a retarded time with respect to the test charge.  To an observer in the q_t frame, q_s is a distance r_t away from q_t at t=0, and is, we will assume, moving directly away from q_s with speed beta = v/c.  What is the separation for an observer in the q_s frame however? 

We need to address a conceptual issue before we can answer this question.  What do we mean by “now” for the q_s observer?  When talking about potentials we must use the retarded positions of the source charges.  Because the q_s charge is moving this makes a difference.  To the q_s observer the retarded position of the q_t charge, the position that the q_s can see, is at a different time (and position) than being calculated by the q_t observer.  To make sense of this question we must have the q_s observer calculate the distance to the advanced position of the q_t charge from the q_s frame.  The problem is to calculate the separation in space between q_t and q_s at two events (space-time positions) that are on a common null line, with q_t in the future wrt q_s.  Below is a Minkowski space-time diagram of the situation, as seen in the q_s frame:

We will arbitrarily designate the coordinates at q_t as being the origin.  We will also specify that the q_s frame space-time origin is at the same place as the q_t origin, at the moment we are calculating.  Thus in the q_t frame the q_s position is, if we align the x axis with r:

Note that we are using space coordinates here.  That is, the time coordinate is being measured in distance.  We use the Lorentz transform to get the q_s position

Thus the spatial separation of the charges in the q_s frame is:

Thus the potential the q_s observer would calculate at the advanced position of q_t is:

Where here phi, the potential, is calculated from the q_s observers point of view to the advanced position of q_t.  In this frame there is no magnetic field.  Thus the potential energy of the interaction does not depend on the speed of the test charge.  It seems reasonable to assume that this energy of interaction will be transformed to the test charge frame via the Lorentz transform, and in fact this gives us the correct answer.

What is this potential as transformed back to the q_t frame?

or

These potentials are called the Lienard-Wiechert Potentials.  The forces on the test charge are then:

Where now phi and A are as calculated in the q_t frame.  The separation is larger in the source charge frame (if it is receding from the test charge), but that increased separation is partially compensated for by the Lorentz transformation from the source to test charge frames.

Note the effect the 1+beta term in the denominator has.  If the source charge is receding at near the speed of light, the potentials, and thus the forces, are reduced by one half.  On the other hand, if the source charge is approaching the test charge at near the speed of light, beta is negative and the potentials, and thus the forces, can be arbitrarily large.

Electromagnetic Forces

Electromagnetic Forces

For the electrostatic case we calculated the force by subtracting the electrostatic potential from the total energy (h_bar omega ).  Let’s try generalizing this and subtract the electromagnetic 4-potential from the test charge energy-momentum 4-vector in the Klein-Gordon equation.  For the time being we will have to restrict ourselves to forces on stationary test charges, but we allow the source charge to move.  This means that in the Klein-Gordon equation the k term is initially zero, but there is a vector potential from the moving source charge:

We are trying to calculate the forces on a free particle.  If the potentials were constant in time this would imply that the total energy (h_bar omega ) is constant as well.  We will not make that assumption this time however.  We will assume that each term above is constant separately.  Let’s solve for omega and k, with the constant value of each term captured as omega_0 and k_0:

Where

Now expand each expression in a Taylor Series about the position r1, with respect to time and space. Keeping just the first linear terms gives:

Where x is the displacement from r₁.  We now put these expressions into the wave function:

We move the gradient of the potential to the k term, as before, to get:

And now take the time derivative of the exponent to get dp/dt, the 4-force:

Or more compactly:

Or, in terms of the 4-vector potential

The first (top) term is the rate of change of energy of the test charge.  We see that this depends only on the rate of change of the electric potential.  The remaining terms are all the conventional electro-magnetic force on a stationary particle.  It depends on the gradient of the electric potential and the rate of change of the magnetic vector potential.

Note that this result is incomplete in that it does not include magnetic forces, which are only apparent when the test charge is moving.  Before addressing magnetic forces, however, we need to derive the relativistically correct way to calculate the 4-potential for a particle moving very fast, at an appreciable fraction of the speed of light.  These are the so-called Lienard-Wiechert potentials.